Тема: Арифметична прогресія, її
властивості. Формула n – го члена арифметичної прогресії.
Мета:
сформувати поняття
арифметичної прогресії, n – го члена арифметичної прогресії, різниці арифметичної
прогресії,
Сформувати вміння
застосовувати поняття та властивості арифметичної прогресії до розв’язування
задач;
Формувати вміння
аналізувати та чітко висловлювати власну думку;
Розвивати логічне
мислення, творчу і розумову діяльність, комунікативні здібності, виховувати
інтерес до математики, увагу, самостійність, формувати вміння працювати з
літературою.
Тип уроку: засвоєння нових знань, умінь та навиків.
Обладнання:
таблиці, дошка, підручник, картки.
Епіграф:
«Недостатньо
мати добрий розум, головне це раціонально його застосовувати»
Р.Декарт
Хід уроку
І. Організаційний етап
Вступне
слово вчителя
Розпочалося вже століття
двадцять перше
То може люди будуть
прагнуть знати менше?
Здається вивчені вже космос
і моря,
Зірок будова і уся земля.
Чи варто зайвий раз
ризикувати?
Заради того, щоб нове щось
взнати?
Я вважаю,що варто.
Мабуть всім відомі
такі істини: перша умова якої треба дотримуватись в математиці - це бути
точним. Друге – бути чітким і наскільки можливо простим.
ІІ. Актуалізація опорних знань.
Діти, згадаймо над
якою темою ми розпочали працювати? (Числові послідовності)
Тож пригадаймо, що ми
вже знаємо стосовно даної теми.
І так
«Бліцопитування». Від вас потребується чітка і лаконічна відповідь. Готові?
«Бліцопитування»
1.
Що
називається числовою послідовністю?
2.
Які
бувають послідовності?
3.
Які
способи завдання послідовностей ви знаєте?
4.
Правило
додавання від’ємних чисел.
5.
Правило
додавання чисел з різними знаками?
6.
Як
називають графік квадратичної функції?
7.
Що
називають відсотком?
8.
Як
відкрити дужки перед якими стоїть знак «-»?
9.
Що означає
розв’яжіть нерівність.
Молодці!!!
ІІІ. Перевірка домашнього завдання
(взаємоперевірка за зразком)
Так, діти, робота в парах під назвою «Перевірка домашнього завдання»,яка
допоможе вам не тільки перевірити матеріал попереднього уроку,а і бути уважним
і відповідальним в прийняті рішень. В основному вас має цікавити правильні відповіді та відповідні
кроки розв’язання останнього завдання. Перевіряючий виставляє оцінку і ставить
свій підпис. Наголошую, у разі завищення оцінки перевіряючому буде знижена оцінка. Враховуйте і те що
оцінки мають відповідати відповідному рівневі .
Підводимо підсумки
перевірки. Підніміть руку у кого 12….
ІV. Постановка теми і мети уроку
А сьогодні на уроці дотримуючись двох умов
математики ми просто,чітко і з легкістю
розглянемо один із видів числової
послідовності - арифметичну прогресію.
І так, тема нашого уроку «Арифметична
прогресія».
Мета уроку:
Сформувати поняття арифметичної
прогресії,різниці арифметичної прогресії, вивести формулу n – го
члена арифметичної прогресії,визначити властивість членів арифметичної
прогресії, показати зв’язок арифметичної прогресії з
іншими дисциплінами.
V. Мотивація навчальної діяльності
Внутрішня
гармонія, строга витончена краса роблять
теорію арифметичної прогресії
відображенням об’єктивного світу,що існує незалежно від нас, нашої свідомості.
Я взяв епіграфом до
нашого уроку, на мій погляд чудові слова видатного математика Р.Декарта
«Недостатньо мати добрий розум, головне це раціонально його застосовувати»
Це і буде на мій погляд мотив для вивчення
даної теми та і взагалі для вивчення математики. Ви, можливо, в майбутньому
поєднаєте своє життя з біологією,так як являєтесь учнями біологічного
класу,тому в процесі уроку я спробую вас
переконати що дана тема поєднується як з біологією так і взагалі з життям.
VІ. Вивчення нового матеріалу
Я пропоную вам
розглянути нову тему за допомогою математичного міні – дослідження. Над даним
дослідженням працюватимуть учні, які прагнуть
мати оцінки достатнього і високого рівнів навчальних досягнень. А решті
учнів, я пропоную працювати над іншим
завданням ,яке називається «Пошук
інформації». Для цього я вам даю чотири ключових питання, а ви в підручнику
на стор. знаходите відповіді на ці питання і розробляєте тези опорного конспекту.
Картки учням
приготовлені і роздані на парти перед початком уроку.
1.Означення арифметичної прогресії.
2.Рекурентна
формула арифметичної
прогресії.
3. Формула
n – го члена арифметичної прогресії.
4.Властивість членів арифметичної прогресії.
І так Міні –
дослідження
Перед вами ряд послідовностей
А)2,5,8,11,14,…
Б)28,38,48,58,…
В)-1,-2,-3,-4,-5,…
Що ви помітили у даних послідовностях? Як можна знайти
кожний член послідовності починаючи з
другого?
Оттаку послідовність і
називають арифметичною прогресією. Попробуйте самостійно сформулювати означення
арифметичної прогресії. Учні пробують сформулювати означення.
Арифметичною прогресією називають числову
послідовності,кожний член якої починаючи з другого, дорівнює попередньому, до
якого додано одне й те саме число.
На
дошці учні бачать означення і коректують свої формулювання. Один учень
читає.
Це число називають різницею арифметичної
прогресії і позначають d.
Якщо різниця прогресії
d
> 0, то прогресія є зростаючою, якщо різниця d < 0,
то прогресія є спадною, а при d = 0 — сталою.
А)1,4,9,16,25….
Б)2,3,4,5,6…..( d=1 )
В)9,11,13,15,…(d=2)
В. Серед
поданих послідовностей укажіть арифметичну прогресію і вкажіть її різницю
Як можна за
допомогою формули записати означення
арифметичної прогресії?
(на дошці учень
записує формулу арифметичної прогресії и різниці)
Таким чином,
арифметичну прогресію можна задати рекурентно.
Усно а1=3,d=-2
Знайдіть
перші чотири члена арифметичної прогресії . Так що нам потрібно знати, щоб
задати арифметичну прогресію?( перший
член і різницю).
А чи зручно буде знайти сотий член
арифметичної прогресії тільки за допомогою цієї формули?(ні) Тому давайте
подумаємо як можна зробити наші обчислення простішими?Вивід формули n – го члена арифметичної прогресії (на дошці один учень).
а2 = а1
+ d
a3 = a2
+ d = (a1 + d) + d = a1 + 2d
a4 = a3
+ d = (a1 + 2d) + d = a1 + 3d
a5 = a4
+ d = (a1 + 3d) + d = a1 + 4d
a6 = a1
+ 5d
...........................................................
an = a1 + d (n – 1)
 А тепер подумаємо , чому прогресію назвали
арифметичною? Розгляньте будь-який член арифметичної прогресії
3,5,7,9,11…. Як він пов'язаний
з його наступним і попереднім членами?
Виявляється,що він дорівнює середньому арифметичному наступного і попереднього членів,тобто
А тепер подумаємо , чому прогресію назвали
арифметичною? Розгляньте будь-який член арифметичної прогресії
3,5,7,9,11…. Як він пов'язаний
з його наступним і попереднім членами?
Виявляється,що він дорівнює середньому арифметичному наступного і попереднього членів,тобто
Звідси
і назва арифметична прогресія і
властивість членів арифметичної прогресії
Питання до учнів які
займалися пошуком інформації.
Питання до учнів які
займалися пошуком інформації
В. ви
бачите перед собою всі формули,які ми вивели а тепер згадаймо ще раз і дамо
назву кожній формулі.
VІІ. Засвоєння нових
знань та умінь
(Робота з підручником)
Тепер спробуємо
набуті знання застосувати на практиці.
1.Усно (за
підручником)
2.Розвязання під керівництвом учителя: (за підручником)
Розв'язок задач практичного напрямку (музика)
Ліси різних порід
випаровують протягом вегетаційного періоду з 1 га різну кількість води . Наприклад:ялиновий ліс-2000 т,буковий-1700
т,дубовий-1400 т.
У нас в районі
розповсюджені дубові ліси. І так мій шановний біологічний клас. До вашої уваги
біологічна задача. (Учень читає)
Задача 1.
Дубовий ліс в травні з
одного гектара випаровує 280 тонн води. Скільки води буде випаровувати такий
ліс в серпні, якщо щомісяця він випаровує на 20 тонн більше. Як впливає
випаровування води лісом на клімат?(Самостійно)
Визвати
учня на закриту дошку, і зробити перевірку.
А можливо у нас є
майбутні медичні працівники? Тож ще одна задача. Давайте розв’яжемо колективно
дану задачу. Одного учня на дошку
визвати по бажанню.
Задача
2.
Кількість еритроцитів (з розрахунку на 1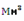 )в крові людини становить на рівні моря 5 млн. через
кожні 600 метрів підняття вгору їх кількість збільшується на 1 млн. скільки
еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест
(4800м)? Чому це відбувається?
)в крові людини становить на рівні моря 5 млн. через
кожні 600 метрів підняття вгору їх кількість збільшується на 1 млн. скільки
еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест
(4800м)? Чому це відбувається?
А наступна задача
пов’язана взагалі з буденністю, давайте її розв’яжемо усно.
Задача
3.
VIII. Підсумок уроку
Ми дуже багато сьогодні з вами виконали різноманітних завдань, тож
давайте зробимо підсумок нашій праці за допомогою вправи
Незакінчене речення
Сьогодні
на уроці ми дізналися про…
Арифметичною прогресією називається…
Якщо різниця
прогресії додатна, то прогресія…
Якщо різниця прогресії
від’ємна, то прогресія…
На уроці я відкрив для себе…
IX. Домашнє завдання
урок добігає кінця і я хотів би ще раз звернутись до нашого епіграфа.
Ви
переконались що дані слова є актуальними?
Чи переконались ви що
дану тему можна пов’язати з майбутньою професією?
Якою саме?
Так , я згоден з вами, ви все правильно розумієте.
Можна не стати великим математиком як Ньютон і Декарт, але вміло застосовувати
знання математики в різних професіях, сферах діяльності людини. Я вдячний вам
за урок.
(Оцінювання)
Розв’язування задач на
використання формул площ квадрата та прямокутника.
Мета:
формувати
уміння і навички розв’язувати задачі практичного і логічного змісту,
використовуючи формули площ;
розвивати
математичну мову учнів, логічне мислення; показати
різноманітне застосування математики в житті; виховувати увагу, самостійність,
активність.
Обладнання: підручник, таблиця «Одиниці вимірювання площ»,
презентація.
Хід уроку
I.
Організаційний
момент.
II.
Перевірка
домашнього завдання.
Вставити пропущені символи у формулах ( умова є на слайді
презентації)
S = __ • b; S = __2 .
III.
Оголошення
теми, мети, завдань уроку
Тема
уроку: Розв’язування
задач на використання формул площ квадрата та прямокутника.
Сьогодні на уроці ми продовжимо
розв’язувати задачі на знаходження площ прямокутника та квадрата, а також
покажемо застосування ваших знань на практиці.
IV.
Актуалізація опорних
знань
Використовуючи формули площ, виконаємо усне обчислення. А
зробимо ми це у формі гри «Математичне
лото». Вибираєте з мішечка число. Під цим числом зашифроване
запитання. Відповідаєте на запитання і переходить черга до наступного учня.
1.
Чому дорівнює площа квадрата, якщо його сторона 20 см. (400 см2)
2.
Сторона квадрата 9 см.
Чому дорівнює його площа? (81 см2)
3.
Скільки м2 в 1 га?
(10000 м2)
5.
Сторони прямокутника 10 см
і 8 см.
Чому дорівнює його площа? (80 см2)
V.
Розв’язування
задач 
На
дошці зображено дві фігури. Потрібно знайти їх площу.
-
Як знайти площу першої фігури?
-
Якою властивістю ви
скористалися?
-
Запишіть розв’язання задачі у
зошитах.
1)
25 – 10 = 15(м) – ширина
більшого прямокутника;
2)
15 · 40 = 600 (м2) –
площа більшого прямокутника;
3)
20 · 10 = 200 (м2) –
площа меншого прямокутника;
4)
600 + 200 = 800 (м2) –
площа фігури.
Відповідь. 800 м2.
-
Як знайти площу другої фігури?
-
У чому відмінність?
-
Зробіть висновки.
(учні записують розв’язання
задачі на дошці і в зошитах)
1)
7 · 9 = 63 (см2) – площа зовнішньої фігури;
2)
4 · 3 = 12 (см2) –
площа внутрішньої фігури;
3)
63 – 12 = 51 (см2) –
площа фігури.
Відповідь. 51 см2.
Розв’язування задач практичного змісту.
Майстру
необхідно кахлем, що має ширину 20см і
довжину 25см, обкласти стіну, ширина якої 250см , а висота - 4м. Скільки потрібно кахлю?
-
Поставте запитання до даної
задачі.
Дану задачу потрібно разом з
учнями змоделювати на задачу математичного змісту. Підвести учнів до використання
саме формул площ.
1) 20 · 25 = 500 (см2)
– площа однієї кахлі;
2) 250 · 400 =
100000 (см2) – площа стіни;
3)
100000 : 500 = 200 (шт.)
Відповідь. 200 штук
кахлю.
VI.
«Домашнє завдання»
VII.
Підсумки уроку.
 А тепер подумаємо , чому прогресію назвали
арифметичною? Розгляньте будь-який член арифметичної прогресії
3,5,7,9,11…. Як він пов'язаний
з його наступним і попереднім членами?
Виявляється,що він дорівнює середньому арифметичному наступного і попереднього членів,тобто
А тепер подумаємо , чому прогресію назвали
арифметичною? Розгляньте будь-який член арифметичної прогресії
3,5,7,9,11…. Як він пов'язаний
з його наступним і попереднім членами?
Виявляється,що він дорівнює середньому арифметичному наступного і попереднього членів,тобто 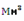 )в крові людини становить на рівні моря 5 млн. через
кожні 600 метрів підняття вгору їх кількість збільшується на 1 млн. скільки
еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест
(4800м)? Чому це відбувається?
)в крові людини становить на рівні моря 5 млн. через
кожні 600 метрів підняття вгору їх кількість збільшується на 1 млн. скільки
еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест
(4800м)? Чому це відбувається?


Немає коментарів:
Дописати коментар